ある、なしの問題
数学的な解釈があるかどうかわかりませんが”ある”と”なし”の問題について紹介します。
宝探しの話
モデルベース開発からかけ離れてしまいますが、昔テレビでも流行った徳川埋蔵金などの宝探しです。
この宝探しというのは多くの場合は”宝があるかも知れない。”ただし、ないかも知れない。”
これが”ある、なしの問題”です。
これの根本的な問題というのは
”宝は実在しているんだろうけど、まだ見つかっていないだけに違いない。”
↓
”だから、見つかるまで探し続ける”
という構造なことです。
実はこの”ある、なしの問題”って言うのがシステム解析で重要になってきます。
”ある”、”ない”の他に”みつかっていない”という3番目の答えがあるからです。
赤城山、すべてを掘り起こすには莫大な時間がかかるのでピンポイントで目星つけて掘り起こすわけです。
システム解析における”ある、なしの問題”
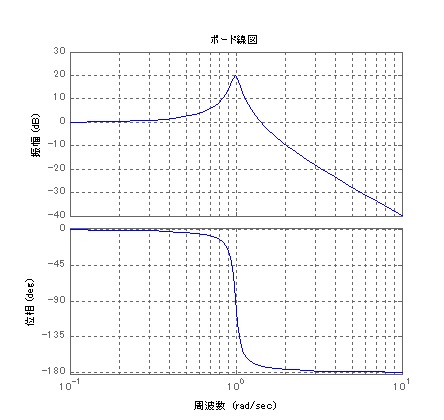
ある条件を与えたうえで”解析的に解く”という手法、例えば振動系を考えた場合に、振動が著しく大きくなる共振点がある系なのかどうか言うのにどういった手法使いますか?
システムが簡単に示される場合は解析解を使って共振曲線を描けばわかります。
もしかすると、過減衰で共振点がないシステムかも知れません。
この場合、代数方程式をとけばすべての解が求められるわけです。
それが定量的かつ、定性的にわかります。この場合、定常振幅を求めるのにシミュレーションせずにωを細かくスイープさせてて共振曲線書けばどこにピークがあるかわかります。
また、G=1/(s^2+0.1s+1)というシステムですが2次式の解き方で特性方程式を解けば
>> (-0.1+sqrt(0.1^2-4*1*1))/2*1
ans =
-0.0500 + 0.9987i
という答えが出ます。
虚数が出てるので共振点をもった振動系で、負の実数部を持つので減衰系であるとわかります。
そして、固有振動数が約1(0.9987)ってことが簡単にわかります。
これが解析解でこの方法では確実に答えが見つかり、もう少し基礎式をいじれば出力の拡大率を求めることができます。
もし、過減衰の場合はどうでしょうか?
>> (-2.5+sqrt(2.5^2-4*1*1))/2*1
ans =
-0.5000
この式を解けば虚数解がなく、負の実数解だけとなるので振動しない減衰系ということがわかります。
では、数値シミュレーションでオイラー法とか使って解を求める場合どうでしょうか?調和入力で評価した場合です。
全ての入力周波数について、シミュレーションをやって数値解を求めることとなります、この場合はめんどくさいので入力周波数を飛び飛びで評価しますよね?
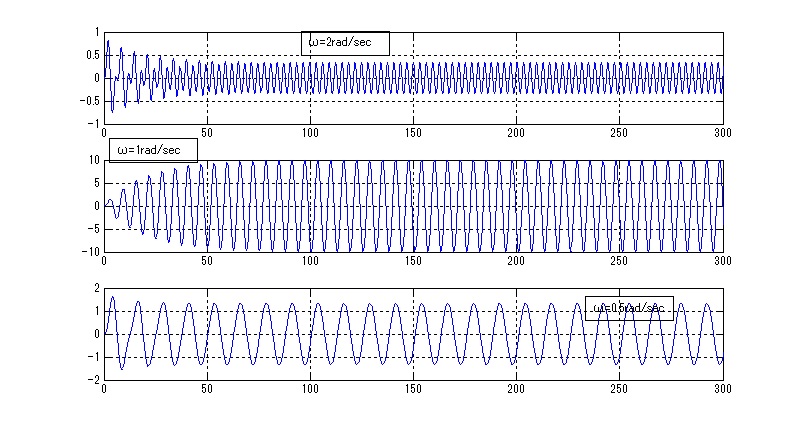
この場合あるシステムに対してω=2,1,0.5を入れてシミュレーションで数値的に求めた。定常振幅が0.33、10、1.33となっている。こうしてωを変化させて何通りもシミュレーションして定常振幅を求めてみる方法が数値的な解放です。とりあえず3点調べてみたらω=1の時が最も定常振幅が大きく、ω=0.5、2の時はそれよりも小さい。⇒きっと共振点は0.5から2の間にあるだろう。
というレベルではわかります。
ちなみに、固有振動数を実験的、数値的に見る方法としては調和入力でなくインパルスとかステップ入力で評価すれば求めることができますが、周波数全域にわたって周波数特性を見るにはやはり調和入力与えないと答えが出てきません。
この場合、すべての解を求めるのであれば膨大な時間がかかってしまいます。またシステムの共振点が見つからなかった場合は過減衰のシステムかもしれないし、単に与えた入力周波数ではたまたま共振点が見つからなかっただけかも知れません。
前者の解析的に求めた場合は、問題ないですが後者の数値的に求めた場合は膨大な時間がかかるうえに
”解があればあったと言える。解がない場合はないのかもしれないし、たまたま見つからなかっただけかも知れない。”
こういった怖さが”ある、なしの問題”にはあります。
ちょっと、話題が解析解と数値解になってしまいましたが、これが数値解法の落とし穴です。
ただ、解析解を得られるほど簡単な構成になっているシステムもありますが、自動車の様にエンジン、トルクコンバータ、トランスミッション、シャフト、タイヤなど考慮するとかなりの強非線形のシステムというのは世の中にはたくさん存在します。
こういったものを解析的に解こうとすると、解くことが不可能なケースがたくさんあります。
ですから、結局数値解を求めなければいけないんですね。
また、仮に複雑なシステムを解析的に解くにはモデリングとして低次元化、線形化を実施して解くことはよくあります。
そして、その解がそこそこ使える場合も多いのですが、現実のシステムに当てはめて考えると”スピルオーバ”という現象に悩まされることがあります。
例えば、柔軟ビームを簡単な1自由度のバネますモデルとして扱った場合、本来は高調波が出やすいので多自由度系で解くことが望ましいけれども強引に低次元化してしまったために、解析的に解が得られても実験すると実際には高調波がでてきてしまう現象です。もちろんモデルで扱うだけなら解析解でも数値解でも高調波が出ませんが・・・
これは別の話ということにしておきます。
結局、詳細なモデリングが難しい場合が多かったら、低次元化してしまうと仮に解析解を求めたとしても実際と異なる場合があるので、解析解を使っても”ある、なしの問題”というのはついて回ることが多いかも知れません。
”ある、なしの問題”の怖さ
先ほど、具体例を示しました。
それ以外にも、系によっては
- 不安定解、不安定領域
- ゼロ割
- 特異点
の”ある、なし”がわかっていればいいのですが、たんに”見つからなかっただけ”ということになればとんでもないエラーを起こす可能性があります。
システム解析の場合だと結局、解析的に解けるものは解析的に解いた方が安心できるってことです。
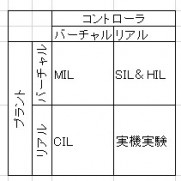
また、ECUに制御プログラムを組み込んだ場合HILのレベルですべての不具合が見つかればいいのですが、バグがあるけど見つからないだけかないのか、本当にないのかというのはモデルベース開発の手法が進めば進むほど気を付けなければいけない問題ですね。
プールで100円落とした。
プールで100円落として、それを探そうとしたら
- 誰かがすでに拾ったかもしれない
- めんどくさいからあきらめる
- 落としてそうなところ見たけど見つからなかった
- そもそも100円落としてなかった
100円落としたのは間違いないから、見つけるためにプールの水を全部抜いて調べる。
- その結果200円見つかった。
- 落としたのは200円だった。
- もしかすると、自分の他にも誰か100円落とした。
数値的に全数を求めるにはプールの100円のみたいな手法をとるということです。
こうすれば”ある”、”ない”だけの問題になりますね。
ちなみに、この”ある、なしの問題”は学生の時に聴いてかなり衝撃受けました。
これは電子回路で”ハイ”、”ロー”で初心者がとらえがちだけど実は”ハイインピーダンス”って状態があるってのも似たようなものかも???



この記事へのコメントはありません。